| Main Heading | Subheadings |
|---|---|
| H1: Understanding Roman Numerals | 1.1 History of Roman Numerals |
| 1.2 Basic Roman Numerals (I, V, X, etc.) | |
| 1.3 How Roman Numerals Work: Additive and Subtractive Rules | |
| H2: Introduction to Multiplication | 2.1 How Multiplication is Represented in Roman Numerals |
| 2.2 Examples of Multiplication in Roman Numerals | |
| H3: Roman Numerals for 35 | 3.1 How to Write 35 in Roman Numerals (XXXV) |
| 3.2 Other Numbers Close to 35 in Roman Numerals | |
| H4: Factors of 35 | 4.1 Definition of Factors |
| 4.2 Prime Factorization of 35 | |
| 4.3 Factors of 35 in Roman Numerals (V and VII) | |
| H5: Multiplication and Roman Numerals | 5.1 Multiplying Roman Numerals: Explanation and Examples |
| 5.2 Challenges with Multiplying Large Roman Numerals | |
| H6: The Roman Numeral System’s Limitations | 6.1 Why Large Multiplications are Complex in Roman Numerals |
| 6.2 The Shift to the Arabic Numeral System for Ease of Calculation | |
| H7: The Legacy of Roman Numerals in Modern Times | 7.1 Roman Numerals in Everyday Life: Clocks, Movies, and More |
| 7.2 The Continued Use of Roman Numerals in Legal and Religious Contexts | |
| H8: How Roman Numerals Shaped Mathematics | 8.1 Influence on Ancient Mathematics and Science |
| 8.2 Transition from Roman to Arabic Numerals and Its Impact on Mathematics | |
| H9: Teaching Roman Numerals Today | 9.1 Why Roman Numerals are Still Taught in Schools |
| 9.2 Methods for Learning and Understanding Roman Numerals | |
| H10: FAQ Section | 10.1 Why is XXXV the Roman numeral for 35? |
| 10.2 How do you multiply Roman numerals? | |
| 10.3 What are the factors of 35 in Roman numerals? | |
| 10.4 How does the Roman numeral system handle multiplication? | |
| 10.5 Why don’t we use Roman numerals for complex calculations today? | |
| 10.6 What are the biggest limitations of the Roman numeral system? | |
| Conclusion | |
| Final Notes and External Links | External links to sources on Roman numerals and their impact |
Roman Numerals That Multiply to 35
H1: Understanding Roman Numerals
Roman numerals have been used since ancient times, originating with the Romans, and they remain prevalent in certain modern contexts. Though they may seem archaic today, roman numerals that multiply to 35 continue to serve ceremonial and practical purposes in various fields.
1.1 History of Roman Numerals
Roman numerals originated from a counting system used in ancient Rome. The system uses combinations of letters from the Latin alphabet (I, V, X, L, C, D, M) to signify different values. The Roman numeral system was developed for trade, record-keeping, and legal documentation.
1.2 Basic Roman Numerals (I, V, X, etc.)
The Roman numeral system is based on the seven main symbols: I, V, X, L, C, D, and M. Each symbol represents a specific value:
- I = 1
- V = 5
- X = 10
- L = 50
- C = 100
- D = 500
- M = 1,000
These symbols can be combined using additive (e.g., VI = 6) or subtractive (e.g., IV = 4) principles to represent numbers.
1.3 How Roman Numerals Work: Additive and Subtractive Rules
In Roman numerals, a smaller numeral placed before a larger numeral subtracts from the larger numeral, while a smaller numeral after a larger numeral adds to it. For example, IV represents 4 (5 – 1), whereas VI represents 6 (5 + 1).
H2: Introduction to Multiplication
In ancient Rome, multiplication was performed differently compared to the arithmetic systems we use today. While multiplication itself was not formally represented by roman numerals that multiply to 35, the numerals still played a role in calculation methods.
2.1 How Multiplication is Represented in Roman Numerals
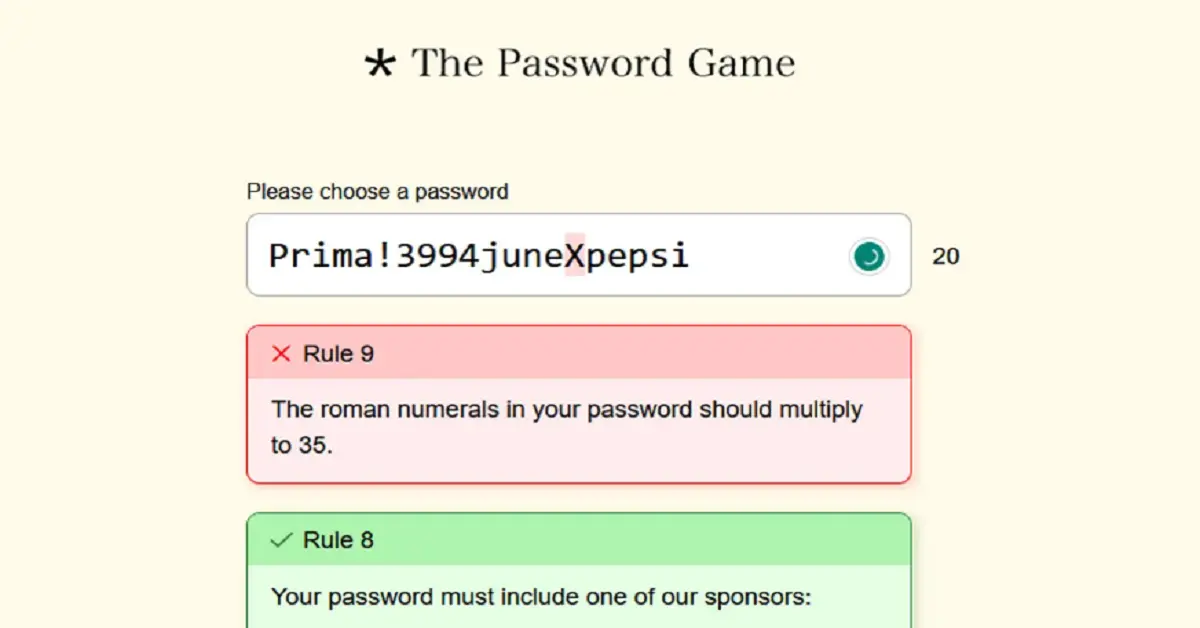
Roman numerals do not have a direct symbol for multiplication, but multiplication can be inferred by repeated addition. For instance, to multiply two numbers, such as 5 × 7, the Romans might have represented this as five groups of VII (7), which totals XXXV (35).
2.2 Examples of Multiplication in Roman Numerals
While there is no multiplication operator in Roman numerals, one can imagine multiplication through repeated addition. For example:
- V × VII (5 × 7) = V + V + V + V + V + V + V = XXXV (35)
H3: Roman Numerals for 35
Roman numerals can represent numbers up to thousands. The number 35 in Roman numerals is expressed as XXXV, where:
- X = 10
- XXX = 30
- V = 5
3.1 How to Write 35 in Roman Numerals (XXXV)
To write the number 35, combine the numeral for 30 (XXX) and the numeral for 5 (V). Thus, XXXV is the Roman numeral for 35.
3.2 Other Numbers Close to 35 in Roman Numerals
Some other nearby numbers include:
- XXXIV = 34
- XXXVI = 36
- XL = 40
H4: Factors of 35
Factors are numbers that can be multiplied together to produce another number. The factors of 35 are important because they help break down the multiplication process.
4.1 Definition of Factors
A factor is any number that divides exactly into another number. For example, the factors of 35 are numbers that multiply to equal 35.
4.2 Prime Factorization of 35
The prime factorization of 35 is:
- 35 = 5 × 7
4.3 Factors of 35 in Roman Numerals (V and VII)
In Roman numerals, the factors of 35 (5 and 7) are written as:
- 5 = V
- 7 = VII
Thus, V × VII = XXXV, which is 35 in Roman numerals.
H5: Multiplication and Roman Numerals
Performing multiplication with roman numerals that multiply to 35 can be tricky because the numeral system lacks a formal structure for multiplication.
5.1 Multiplying Roman Numerals: Explanation and Examples
Multiplication in Roman numerals must be done manually, often using repeated addition or relying on tables. For example, multiplying V (5) and VII (7) would result in XXXV (35) after repeated additions.
5.2 Challenges with Multiplying Large Roman Numerals
One of the challenges of multiplying large roman numerals that multiply to 35 is the lack of positional value, which makes multiplication cumbersome and complex.
H6: The Roman Numeral System’s Limitations
The Roman numeral system, while functional for smaller numbers, faces significant limitations when applied to larger calculations, particularly multiplication and division.
6.1 Why Large Multiplications are Complex in Roman Numerals
Without a positional system, large multiplications require repeated addition, which becomes tedious and error-prone. This is why the Roman numeral system eventually gave way to the more efficient Arabic numeral system.
6.2 The Shift to the Arabic Numeral System for Ease of Calculation
The Arabic numeral system, with its use of zero and positional notation, made arithmetic much simpler, leading to its widespread adoption and the eventual decline of Roman numerals for mathematical operations.
H7: The Legacy of Roman Numerals in Modern Times
Despite their limitations, roman numerals that multiply to 35 still hold a place in modern culture, primarily for symbolic and ceremonial purposes.
7.1 Roman Numerals in Everyday Life: Clocks, Movies, and More
Roman numerals appear frequently in clocks, movie titles, and sporting events like the Super Bowl (e.g., Super Bowl LV for 55). They remain a visually distinct and historically significant way of representing numbers.
7.2 The Continued Use of Roman Numerals in Legal and Religious Contexts
In legal documents and religious texts, Roman numerals are often used to denote sections, chapters, or important events, carrying forward their ancient legacy.
H8: How Roman Numerals Shaped Mathematics
The Roman numeral system, though eventually replaced by the more efficient Arabic numerals, played a significant role in the early development of mathematics in ancient Rome and beyond. Its structure influenced early arithmetic operations and served as the foundation for many early counting and calculation systems.
8.1 Influence on Ancient Mathematics and Science
Roman numerals were pivotal in the administration of the vast Roman Empire. Taxes, trade, military logistics, and building projects all relied on accurate accounting, and the Roman numeral system provided the basis for these operations. Though limited in its capacity for complex arithmetic, the system allowed for basic operations such as addition, subtraction, and simple multiplication. Roman engineers and architects, responsible for impressive feats like aqueducts, roads, and buildings, would have used this numeral system to track measurements and resources.
8.2 Transition from Roman to Arabic Numerals and Its Impact on Mathematics
As Roman civilization declined, scholars in the Middle East, particularly in the Islamic Golden Age, advanced mathematics by adopting and improving upon earlier number systems. The Arabic numeral system, which introduced the concept of zero and place value, allowed for more complex calculations, including advanced multiplication and division.
H9: Teaching Roman Numerals Today
Although the Roman numeral system is no longer widely used for mathematical purposes, it is still taught in many educational systems worldwide. Understanding roman numerals that multiply to 35 offers students a glimpse into the history of mathematics and provides a foundation for understanding ancient texts, artifacts, and architectural designs.
9.1 Why Roman Numerals are Still Taught in Schools
Learning Roman numerals helps students develop problem-solving skills and an appreciation for historical methods of counting and calculation. Many educational curriculums introduce Roman numerals in elementary grades as part of a broader introduction to number systems.
9.2 Methods for Learning and Understanding Roman Numerals
Common teaching methods for Roman numerals include games, puzzles, and historical exercises that engage students with the system in an interactive way. Teachers often use examples from modern life, such as reading clock faces, understanding dates in movies, or Roman numerals used in monarchial titles like “Queen Elizabeth II” (Queen Elizabeth the Second).
Conclusion
The roman numerals that multiply to 35 system, despite its limitations, played a crucial role in the history of mathematics and remains a fascinating subject of study today. While its use for mathematical calculations has been replaced by more efficient systems, roman numerals that multiply to 35 persist in everyday life, whether on clock faces, in book chapters, or on historical buildings.